ФИЗИЧЕСКИЕ ОСНОВЫ МАГНИТНОГО КОНТРОЛЯ НАПРЯЖЕННОГО СОСТОЯНИЯ МЕТАЛЛА ИНДИКАТОРАМИ МЕХАНИЧЕСКОГО НАПРЯЖЕНИЯ

 

Общий физический принцип неразрушающего контроля механических напряжений металла заключается в зависимости т.н. структурно-чувствительных параметров металла от величины механических напряжений.

Остаточная намагниченность металла J_r является одним из таких параметров, обладая при этом наиболее высокой чувствительностью к механическим напряжениям и восприимчивостью к их изменениям.

Намагниченность возникает в стальном изделии при воздействии на него магнитного поля. В сильных полях H_S величина намагниченности изделия может достичь своего предельного значения J_S, такое магнитное состояние называется техническим насыщением (рис.1). После прекращения воздействия магнитного поля, изделие остается в намагниченном состоянии, количественной мерой которого является остаточная намагниченность J_r.

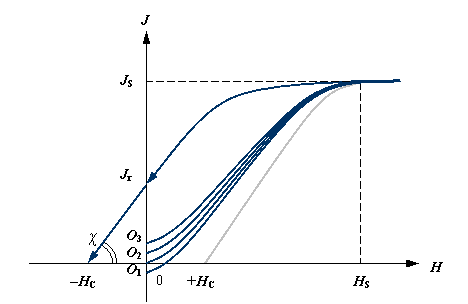
Изменение намагниченности стального изделия J при воздействии на него постоянным магнитным полем H

O_1-3 – спонтанная намагниченность металла в магнитном поле Земли;

H_S – величина напряженности магнитного поля, достаточного для намагничивания изделие до состояния технического насыщения, количественной мерой которого является намагниченность насыщения J_S

J_r – остаточная намагниченность стального изделия после прекращения воздействия на него магнитного поля;

H_C – коэрцитивная сила

 

В индикаторах механического напряжения металла намагничивающее устройство осуществляет намагничивание исследуемого объекта, а измерительное устройство измеряет напряженность (индукцию) поля остаточной намагниченности на поверхности исследуемого объекта, которая, в сущности, является реакцией металла на воздействие намагничивающего устройства.

По отношению к механическим напряжениям остаточная намагниченность металла может проявлять себя как два принципиально разных физических параметра, в зависимости от внешних условий и порядка их влияния на процесс формирования остаточной намагниченности.

Условие 1. При намагничивании элементарного объема металла, подвергнутого воздействию постоянной нагрузки, выполняется соотношение между его основными магнитными параметрами:

,                                     (1)

где χ – магнитная восприимчивость металла, λ_S – магнитострикция насыщения, J_S – намагниченность насыщения, σ – механическое напряжение, μ₀ – магнитная постоянная.

Для прямоугольного треугольника O-J_r-H_C на рис.1 выполняется  геометрическое соотношение, подстановка которого в формулу (1) приводит к следующему равенству:

.                                 (2)

В полученной формуле (2) присутствуют два параметра, зависящие от механического напряжения металла: J_r и Н_С. Для исключения последнего из формулы (2) воспользуемся известной аналитической зависимостью между коэрцитивной силой и остаточной намагниченностью металла:

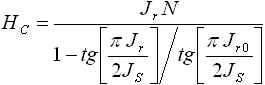,           (3)

где J_r0 – остаточная намагниченность металла при полном отсутствии механических напряжений (σ = 0). Подставляя выражение (3) в (2), и учитывая при этом, что для конструкционных сталей J_r << J_S (см. рис.1), получаем зависимость остаточной намагниченности от механического напряжения металла, подвергнутого воздействию постоянной нагрузки:

.                     (4)

Напряженность поля остаточной намагниченности металла, измеряемая индикаторами механического напряжения, прямо пропорциональна остаточной намагниченности, при этом ее значение зависит от формы контролируемой поверхности: H_r(s) = J_r(s)·TF(x, y, z).

Топографическая функция TF(x, y, z), описывающая контролируемую поверхность, остается неизменной, поэтому зависимость H_r(s) имеет вид:

.                    (5)

В общем случае параметр σ представляет собой эффективное механическое напряжение металла, которое определяется в теории прочности и сопротивлении материалов через компоненты главных напряжений и коэффициенты Пуассона:

.               (6)

В случае линейного (одноосного) напряженного состояния металла (_y = 0 _z = 0), эффективное напряжение равно одной из компонент главных напряжений:.

На рис.2 приводятся экспериментальные зависимости напряженности поля остаточной намагниченности от механического напряжения металла, полученные при линейном (одноосном) нагружении стальных образцов, изготовленных из конструкционных сталей, широко применяемых в промышленности, которые хорошо согласуются с формулой (5).

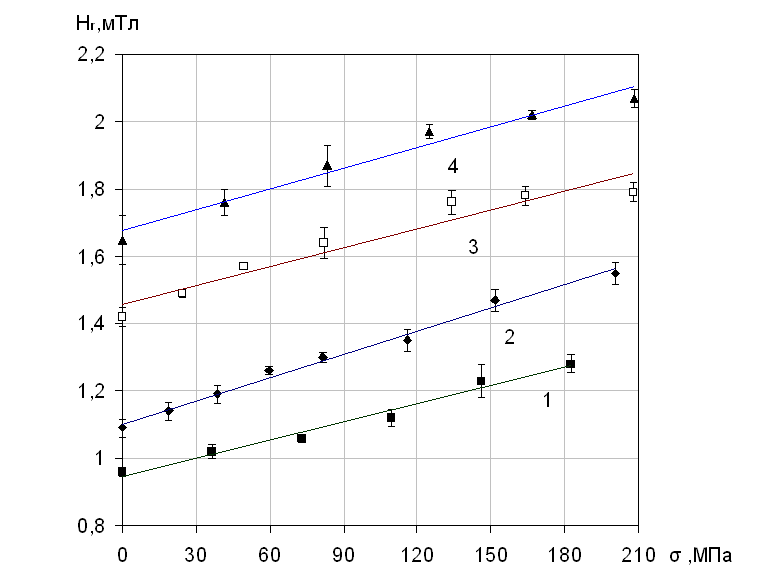
Рис.2. Зависимости напряженности поля остаточной намагниченности от механического напряжения линейно нагруженных стальных образцов

1 – образец из стали Ст3, 2 – ВСт3сп, 3 – 09Г2С, 4 – 17Г1С

 

В случае плоского (двухосного) напряженного состояния металла _z = 0, эффективное напряжение равно, при этом формула (5) примет следующий вид:

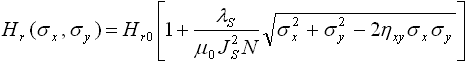.        (7)

Из полученной формулы (7) следует, что характер зависимости напряженности поля остаточной намагниченности металла H_r от компонент главных напряжений σ_x и σ_y определяется соотношением их знаков:

– Если компоненты σ_x и σ_y имеют противоположные знаки, то знак перед коэффициентом Пуассона в формуле (7) становится положительным, при этом зависимость H_r(σ_x, σ_y) имеет однозначный, но нелинейный характер (см. рис.3, σ_x /σ_y < 0);

– Если компоненты σ_x и σ_y имеют одинаковые знаки, то знак перед коэффициентом Пуассона в формуле (7) остается отрицательным, при этом зависимость H_r(σ_x, σ_y) становится неоднозначной (см. рис.3, σ_x /σ_y > 0).

σx /σy < 0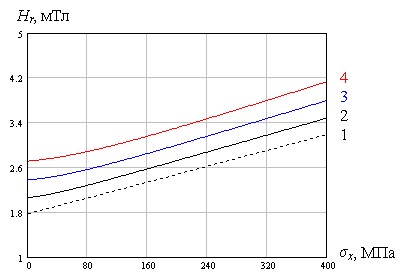

σx /σy > 0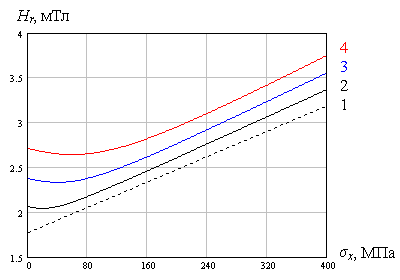

Рис.3. Влияние соотношения знаков компонент σ_x и σ_y плоского напряженного состояния металла на характер зависимости от них напряженности поля остаточной намагниченности H_r

1 – σ_y = 0 МПа, 2 – 40 МПа, 3 – 80 МПа, 4 – 120 МПа

 

Условие 2. При нагружении предварительно намагниченного до технического насыщения элементарного объема металла вследствие магнитоупругого эффекта происходит его размагничивание. При этом напряженность поля остаточной намагниченности металла в области упругой деформации металла изменяется по закону обратной пропорциональности:

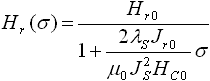,                     (8)

где σ в общем случае представляет собой эффективное напряжение металла (6), которое в случае линейного (одноосного) напряженного состояния металла (_y = 0 _z = 0), равно одной из компонент главных напряжений:.

На рис.4 показано изменение напряженности поля остаточной намагниченности металла при линейном (одноосном) нагружении предварительно намагниченных стальных образцов, изготовленных из конструкционных сталей, широко применяемых в промышленности, которые хорошо согласуются с формулой (8).

В случае плоского (двухосного) напряженного состояния металла _z = 0, эффективное напряжение равно, при этом формула (8) примет следующий вид:

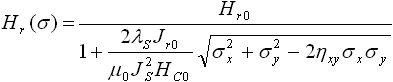.               (9)

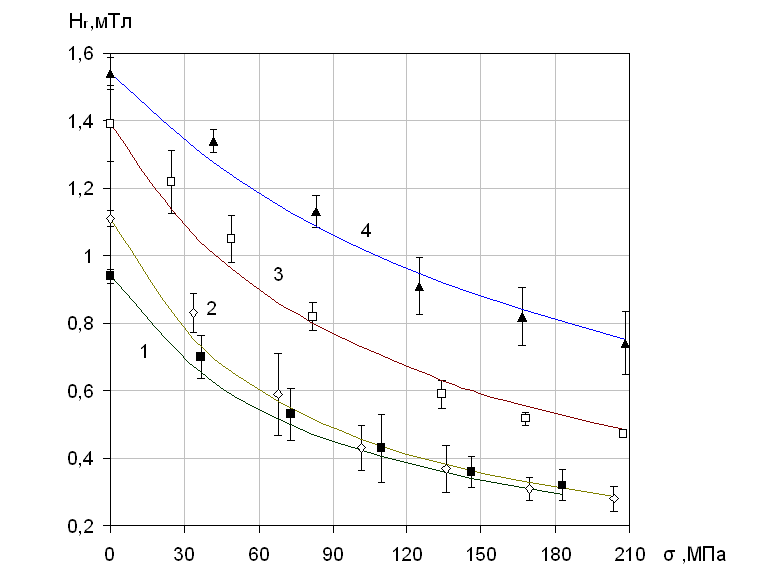
Рис.4. Изменение напряженности поля остаточной намагниченности при линейном нагружении предварительно намагниченных стальных образцов

1 – образец из стали Ст3, 2 – ВСт3сп, 3 – 09Г2С, 4 – 17Г1С

 

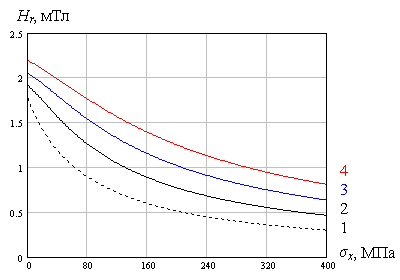
Из полученной формулы (9) следует, что при двухосном нагружении предварительно намагниченного металла характер изменения напряженности поля остаточной намагниченности H_r определяется соотношением знаков компонент главных напряжений σ_x и σ_y (см. рис.5).

σ_x /σ_y < 0                                                      σ_x /σ_y > 0

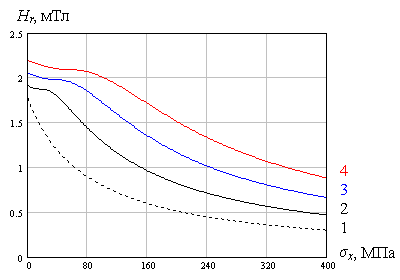Рис.5. Влияние соотношения знаков компонент плоского напряженного состояния металла на характер изменения напряженности поля остаточной намагниченности при двухосном нагружении предварительно намагниченного металла

1 – σ_y = 0 МПа, 2 – 40 МПа, 3 – 80 МПа, 4 – 120 МПа

 

Таким образом, создавая на практике разные начальные условия, можно наблюдать, как напряженность поля остаточной намагниченности металла H_r, измеряемая индикаторами ИН-01м и ИН-02, проявляет себя как два различных физических параметра:

1. При намагничивании стального изделия, подвергнутого воздействию постоянной нагрузки, напряженность поля остаточной намагниченности H_r линейно зависит от величины эффективного напряжения металла σ_э; при этом зависимость H_r от компонент главных напряжений σ_x и σ_y имеет более сложный характер, который определяется соотношением их знаков.

2. При нагружении предварительно намагниченного стального изделия напряженность поля остаточной намагниченности металла H_r в области упругой деформации изменяется по закону обратной пропорциональности.

Рис.6. Лабораторная тензометрическая установка для экспериментального исследования двухосного напряженного состояния металла

1 – исследуемый стальной образец, 2 – силовые винты, 3 – тензометрические преобразователи, 4 – контрольно-измерительный модуль

 

В настоящее время наши специалисты проводят экспериментальную проверку теоретически полученных зависимостей напряженности поля остаточной намагниченности H_r от компонент главных напряжений σ_x и σ_y на специально разработанной для этой цели тензометрической установке, показанной на рис.6.